如图a所示是一个处于竖直平面内的特殊运动轨道,OA是长为x
1=2R的直轨道,AE是倾角为30°的斜轨道,它们与滑块的动摩擦因数为
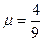
,EDF是圆心在B点,半径为R的光滑圆弧,D点是最高点,ED圆弧上方有一个高度与滑块相近的光滑圆弧形挡板PQ,轨道上的A、E两点理想连接,使滑块经过这两点时不损失机械能,且AE⊥EB可视为质点的滑块,质量为m,以v
0的初速度从O点进入OA直轨道,滑块在OA轨道运动时,受到水平向右的动力作用,它的大小随滑块与O点的距离变化,如图b所示,图中F
0=mg滑块经A点滑上斜轨道,到达轨道最高点D时恰好对轨道和挡板都无压力,此时立刻撤除圆弧形挡板PQ滑块经D点后能无碰撞地进入一个特殊的漏斗C,漏斗C能将滑块以进入时的速率反向弹出,求:

小题1:滑块在D点时的速度大小;
小题2:初速度v
0的大小;
小题3:滑块从漏斗C中弹出后会再次经过D点吗?若会经过D点,请求出经多长时间再次到达D点,漏斗离F点的x
2多大?若不会经过D点,请说明理由。

