解:(1) 振子在平衡位置时,所受合力为零,
设此时弹簧被压缩Δx
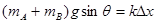
……1′
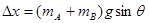
/
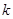
=10cm……1′
释 放 时振子处在最大位移处,故振幅A为: A=10cm+10cm=20cm……2′
(2)由于开始时弹簧的伸长量恰等于振子在平衡位置时弹簧的压缩量,
故弹簧势能相等,设振子的最大速率为v,
从开始到平衡位置,根据机械能守恒定律:
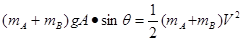
……2′
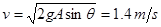
……2′
(3)在最低点,振子受到的重力分力和弹力方向相反,根据牛顿第二定律:
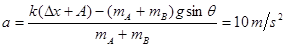
……1′
A对B的作用力方向向上,其大小
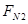
为:
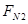
=

=15N……2′
在最高点振子受到的重力分力和弹力方向相同,根据牛顿第二定律:
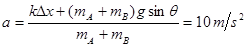
……1′ (或由对称性可得)
A对B的作用力方向向下,其大小
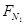
为:
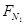
=

=5N……2′
本题考查简谐运动,要求振子的最大振幅,即释放振子的位置就是最大振幅位置,关键是求出释放位置距离平衡位置的距离,由于在平衡位置回复力等于零即重力的下滑力等于弹簧的弹力,列等式可求出平衡位置时弹簧的压缩程度,即可求出振幅,整个过程中,重力和弹簧弹力做功,所以机械能守恒,要求最大速度,即在平衡位置时的速度,由于开始时弹簧的伸长量恰等于振子在平衡位置时弹簧的压缩量,故弹簧势能相等,可根据机械能守恒,列出等式求解,在最低点,振子受到的重力分力和弹力方向相反,在最高点振子受到的重力分力和弹力方向相同。根据牛顿第二定律可解。

