如图所示的皮带传动装置中，右边两轮是在一起同轴转动，图中A、B、C三轮的半径关系为RA=RC=2RB，设皮带不打滑，则三轮边缘上的一点线速度之比vA：vB：vC=______，角速度之比ωA

首页 > 考试 > 物理 > 高中物理 > 线速度/2022-09-22 / 加入收藏 / 73 阅读 [打印]
闂備胶鍎甸崜婵堟暜閹烘绠犻幖杈剧悼閸楁岸鏌ら崫銉︽毄闁荤喎缍婇弻娑⑩€﹂幋婵囩亪闂佺粯甯楀浠嬬嵁閺嶎偀鍋撳☉娅辨粍绂掗敂鍓х＜婵°倐鍋撻柟铏悾鐑芥晸閻樻彃宓嗗┑顔矫畷顒勫几閻樼粯鈷戦悹鍥ｂ偓宕囦紙闂佺懓鍤栭幏锟� 濠电姵顔栭崳顖滃緤閻ｅ本宕查柟鐗堟緲妗呮繝銏ｆ硾椤戞垹妲愰敐澶嬬厱闁斥晛鍠氬▓鏃傜磼閹绘帗鍋ラ柡灞剧洴楠炴帒鈹戦崱鏇炴瀳闂備浇妗ㄧ粈渚€鏁冮妷銉＄細濠电姵鑹鹃悙濠傤渻鐎ｎ亝鎹ｆい锔诲櫍濮婃椽宕ㄦ繝搴㈢暦濠电偛寮堕悧鏇㈡偩閻戣姤鍋勭紒瀣儥閸ゃ倕鈹戦埥鍡楃仴妞ゆ泦鍥х闁哄洨浼濋悷鎵冲牚閹肩补鈧尙鏆楃紓鍌欑劍椤ㄥ懘藝闂堟稓鏆﹂柟杈鹃檮閺呮悂鏌ㄩ悤鍌涘

◎ 题目

如图所示的皮带传动装置中，右边两轮是在一起同轴转动，图中A、B、C三轮的半径关系为RA=RC=2RB，设皮带不打滑，则三轮边缘上的一点线速度之比vA：vB：vC=______，角速度之比ωA：ωB：ωC=______．
魔方格

◎ 答案

由于A轮和B轮是皮带传动，皮带传动的特点是两轮与皮带接触点的线速度的大小与皮带的线速度大小相同，
故vA=vB，
∴vA：vB=1：1
由角速度和线速度的关系式v=ωR可得
ω=
v
R

ωA：ωB=
vA
RA
vB
RB
=
RB
RA
=1：2
由于B轮和C轮共轴，故两轮角速度相同，
即ωB=ωC，
故ωB：ωC=1：1
ωA：ωB：ωC=1：2：2
由角速度和线速度的关系式v=ωR可得
vB：vC=RB：RC=1：2
∴vA：vB：vC=1：1：2
故答案为：1：1：2，1：2：2．

◎ 解析

“略”

◎ 知识点

    专家分析，试题“如图所示的皮带传动装置中，右边两轮是在一起同轴转动，图中A、B、C三轮的半径关系为RA=RC=2RB，设皮带不打滑，则三轮边缘上的一点线速度之比vA：vB：vC=______，角速度之比ωA…”主要考查了你对  【线速度】，【角速度】  等知识点的理解和应用能力。关于这些知识点的“档案”，你可以点击相应的链接进行查看和学习。

闂佺儵鍓濈敮鎺楀箠鎼达絿鍗氶柤鍝ユ暩閻熷綊鏌涢…鎴濇灈闁绘帗妞介獮鏍偓娑櫱滄禒锔剧磼濡も偓閹虫ê鐣烽敓鐘插嵆婵ê宕弸鐘绘⒑鐠団€崇伈闁瑰嚖鎷� 婵犳鍣徊鐣屾崲閹版澘桅濠㈣泛顑戠槐锝夋煕閳╁喚娈旂紒鎻掓健閺屾盯骞掑┑鍡曞枈闂佽桨绀侀敃銉メ缚婵犳艾鐐婂瀣捣椤︻噣姊洪崨濠庢畷婵炲弶鐗曢悾鐑芥偄缁嬫鍤ゅ┑鈽嗗灥椤曆囧礉閺囩伝鐟扳堪鎼粹€茬暗缂備焦顨呴ˇ闈涚暦閹达附鏅搁柨鐕傛嫹
三轮 一点 打滑 同轴 知识点
  • 最新内容
  • 相关内容
  • 网友推荐
  • 图文推荐
  • 如图所示，倒置的光滑圆锥面内侧，(2022-09-22)
  • 甲、乙两名溜冰运动员质量分别为80(2022-09-22)
  • 如图所示，有一长为L的细线，细线的(2022-09-22)
  • 如图所示，内壁光滑的圆台形容器固(2022-09-22)
  • 如图所示，位于竖直面内的曲线轨道(2022-09-22)
  • 如图所示，在皮带传动装置中，主动(2022-09-22)
  • 质量为m的小球用长为L的悬线固定在(2022-09-22)
  • 如图所示，质量m＝1kg的小球用细线(2022-09-22)
  • 关于角速度和线速度，说法正确的是(2022-09-22)
  • 在如图所示的传动装置中，已知大轮A的半径是小轮B半径
  • 如图所示，在轮C上固定有同轴小轮A，轮C通过皮带带动轮
  • 如图所示的皮带传动装置中，已知两轮半径的关系为r1=2
  • 如图传送带不打滑，圆A的半径为圆B的半径的两倍，则圆
  • 如图所示在皮带传动中，右轮半径比左轮半径大．已知它
  • 如图为皮带传动示意图，假设皮带没有打滑，R＞r，则下
  • 如图所示的皮带传动装置，主动轮O1上两轮的半径分别为
  • 如图所示皮带转动轮，大轮直径是小轮直径的3倍，A是大
  • 如图所示的传动装置中，已知大轮A的半径是小轮B半径的
  • 如图所示，轮O1、O3固定在同一转轴上，轮O1、O2用皮带
  • 1920年科学家斯特恩测定气体分子速(2022-09-22)
  • 轻杆长为2l，水平转轴装在中点O处，(2022-09-22)
  • 如图所示，有一皮带传动装置，A、B(2022-09-22)
  • 如图所示的传动装置中，B、C两轮固(2022-09-22)
  • 一质点做匀速圆周运动，下列物理量(2022-09-22)
  • 普通洗衣机的脱水桶以1200r/min的速(2022-09-22)
  • 如图为一皮带传动装置．左轮半径为(2022-09-22)
  • 如图所示，O1、O2为两个皮带轮，O1(2022-09-22)
  • 如图所示，为A、B两质点做匀速圆周(2022-09-22)
  • 如图所示，在皮带传动装置中，主动(2022-09-22)
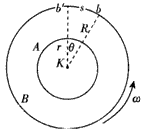
    • 1920年科学家斯特恩测定气体分子速率的装置如图所示，A，B为一双层共轴圆筒形容器，外筒半径为R，内筒半径为r，可同时绕其几何轴经同一角速度ω高速旋转，其内部抽成真空，沿
    1920年科学家斯特恩测定气体    		轻杆长为2l，水平转轴装在中点O处，两端分别固定着小球A和B。A的质量为m，B球的质量为2m，在竖直平面内做匀速圆周运动。当杆绕O以某一速度转动时，A球在最高点，如图所示，此
    轻杆长为2l，水平转轴装在中    		如图所示，有一皮带传动装置，A、B、C三点到各自转轴的距离分别为RA、RB、RC，已知RB=RC=RA/2，若在传动过程中，皮带不打滑。则[]A、A点与C点的角速度大小相等B、A点与C点的
    如图所示，有一皮带传动装置    		如图所示的传动装置中，B、C两轮固定在一起绕同一轴转动，A、B两轮用皮带传动，三轮的半径关系是ra=rc=2rb。若皮带不打滑，求A、B、C轮边缘的a、b、c三点的角速度之比和线速
    如图所示的传动装置中，B、C    		普通洗衣机的脱水桶以1200r/min的速度高速旋转，为避免发生人身伤害事故，脱水机构都装有安全制动系统．如图所示为脱水制动示意图，该系统由脱水桶盖板、制动钢丝、刹车制动盘
    普通洗衣机的脱水桶以1200r/
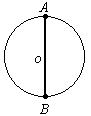
    上一篇：如图所示，一个内壁光滑的圆锥形筒的轴线垂直于水平面，圆锥筒固定不动，有两个质量相等的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动，则以下说法中正确的是     下一篇：天文学上把两个相距较近，由于彼此的引力作用而沿各自的轨道互相环绕旋转的恒星系统称为“双星”系统，设一双星系统中的两个子星保持距离不变，共同绕着连线上的某一点以不同的
    零零教育社区：论坛热帖子
    • 5
    • 4
    • 3
    • 2
    • 1
    闂備礁鎲″濠氬疾濠婂牜鏁勭€广儱妫庢禒姘舵煕濞嗘兛鎴︽儑閽樺妲堥柟鎹愭珪瀹告繂霉鐏忔牕浜鹃梻浣虹帛椤ㄥ棝宕橀懡銈嗩潟婵犻潧鏌婅閹垽宕妷顔兼櫍婵犵數鍋為幆灞剧閿濆绠俊銈勮兌閳绘棃鏌嶈閸撴瑩鍩㈤挊澶嗘瀻闁规儳纾懜褰掓⒑闂堟稒顥滈柛濠勬嚀铻為柍鍝勬噺閳锋劕顭跨捄鐑樺暈濠碘姍鍛亾閸忓浜炬繛鎾村焹閸嬫挻淇婇锛勭煓鐎殿噮鍓涘☉鐢稿椽娴ｅ湱绉块梻浣瑰缁嬫垶绺介弮鍌濆С闁靛⿵绠戠欢鐐垫喐瀹ュ鈧懓顦崇€垫澘瀚伴崺锟犲川椤撶喐姣夊┑鐐茬摠缁絿绱撳杈潟闁靛牆顦繚闂佺ǹ鏈划搴㈡櫠椤忓牊鐓涘璺猴功娴犳盯鏌￠崱蹇婂亾閺傘儲鐏侀柣搴秵閸嬪棛绮婚幒鏂哄亾鐟欏嫭鍊愰柡鈧崡鐑囪€块柍褜鍓熼弻銊モ槈濡警娈紓浣靛妼閸熷潡锝炶箛姘兼Ъ闂佺灏欓崑銈夊箯閸愵喗鍤嶉柕澶涢檮閻濇岸姊洪幖鐐插姶闁告﹢绠栭敐鐐哄箛閺夎銉╂煕鐏炲彞绶遍柛搴耿閺屻倝宕ㄦ繝鍌滎儎闂侀€炲苯鍘搁柤瀹犳硾閳瑰啴宕掗悙鑼潉闂佺粯枪瀹曚絻銇愰姘肩唵閻犲搫鎼鐢电磼鏉堛劎绠橀柍褜鍓涢幊鎾凰囬婊勵偨闂侇剙绉寸粈鍌炴煕閹伴潧鏋ら柣鎴畵閺岋綀顦抽柛搴㈠▕瀵即宕掑В鍏兼⒒缁厾鎮伴垾鍏呭闂佽法鍣﹂幏锟�
    栏目导航
    婵犵數濮烽弫鎼佸磻濞戞﹩鍤曢柛顐ｆ礃閸庡孩銇勯弽顭戝殼闁挎繂妫涢梽鍕磼鐎ｎ偄顕滄俊宸墴閺岀喖宕楅懖鈺傛闂佸憡鏌ㄩ懟顖炲煝瀹ュ鏅搁柣妯哄暱娴狀厼鈹戦悙鍙夘棞婵﹫绠撳畷妤冧沪娣囧彉绨诲銈嗗姧缁茶姤鎱ㄩ崼鐔翠簻闁挎梹鍎抽。濂告煙椤栨稒顥堟い銏＄☉楗即宕担鍓愩儱鈹戦悩鍨毄闁稿绋戣灋婵犲﹤鍠氶崵鏇㈡煙閹冾暢缂佲偓婵犲洦鐓涢柛鎰╁妼閳ь剛鏁诲畷鎴﹀箻閼搁潧鏋傞梺鍛婃处閸撴岸鎮楅鐐粹拺闁告稑锕ラ埛鎺楁煕閻樺磭澧甸柣娑卞櫍瀹曞爼顢旈崱娆愭緫闂佺澹堥幓顏嗙礊閸℃ê顕辨繝闈涱儐閳锋帒霉閿濆洦鍤€缂佽尪宕电槐鎺撳緞鐎ｎ剙寮ㄩ梺绯曟杹閸嬫挸顪冮妶鍡楀潑闁稿鎹囬弻娑欑節閸愨晛鈧劙鎸婂┑瀣厸閻忕偠顕ч崝姘辩磼閻樺啿娴柡宀€鍠栭弻鍥晝閳ь剚鏅堕鈧弻锝夋晜閹冨箣闂佸搫鏈惄顖氼嚕閸婄噥妲煎銈冨劗閸撴繈濡甸崟顖氬嵆婵°倓鐒﹂悵鏇犵磽娴ｅ壊鍎忔い锔诲灦椤㈡ɑ绺界粙鍨獩濡炪倖妫佹慨銈夘敂閿濆鈷掑ù锝囨嚀椤曟粎绱掔€ｎ偄鐏撮柟顖氭湰缁楃喖鍩€椤掑嫬违濞撴埃鍋撴鐐差儔閹瑥鈻撻幐搴ㄦ暅闂備礁鎼ˇ閬嶅磻閻愬樊鐔嗘慨妞诲亾閽樻繈鏌＄仦璇插姕闁绘挻娲樼换娑㈠幢濡搫顫岄梺璇茬箞閸庢娊鍩€椤掍緡鍟忛柛锝忕到宀ｈ儻顦规い銏″哺閺佹劖寰勬繝鍕Е婵＄偑鍊栫敮鎺楀磹閻戣姤鍊垮┑鐘蹭紖瑜版帗鏅查柛銉ㄥ煐濮ｅ矂姊虹粙娆惧剱闁圭懓娲顐﹀箻缂佹ɑ娅㈤梺璺ㄥ櫐閹凤拷
    缂傚倸鍊搁崐鎼佸磹缁嬫５娲Χ閸♀晜顔旂紓浣割儐閿涙洖煤椤忓懎浜滅紓浣割儓濞夋洜绮ｉ悙鐑樷拺闁告繂瀚惂渚€鏌涢幇鍏告喚婵″弶妞藉缁樻媴閽樺姹楅柣蹇撶箞閸旀垿鐛箛娑欐櫢闁跨噦鎷� 闂傚倸鍊烽懗鍓佸垝椤栫偛绀夋慨妞诲亾闁挎繄鍋炲鍕箛椤掆偓閻庮厼鈹戦悩璇у伐閻庢艾鎽滃Σ鎰版晲婢跺鍘遍梺鏂ユ櫅閸犳艾鈻撻弮鍌滅＜闁圭粯甯炴禒銏°亜椤撶偞鍋ョ€规洖銈稿畷鍗炍旀担鎭掑亹闂備礁鎼ˇ鍐测枍閿濆洦顫曢柟鐑樻尵閳瑰秹鏌涘Δ鍐ㄤ户濞寸姴銈搁弻锝嗘償閿濆孩娈伴梺鐟板殩閹凤拷
    闂傚倸鍊风粈渚€骞夐敍鍕瀳鐎广儱娲ㄩ惌娆撴煙鏉堥箖妾柛瀣ㄥ€栫换娑㈠幢濡纰嶉梻浣斤骏閸婃繈寮婚妸鈺佸嵆婵﹢纭稿Σ顔嘉旈悩闈涗杭闁搞劋绮欏濠氬Χ閸ャ劌鏋傞梺鎸庣箓濡厼岣块幇顔剧＝濞达絼绮欓崫铏圭磼鐠囨彃顏紒鍌氱Т椤垹鐣濋埀顒勬偪閳ь剟鏌熼崗鑲╂殬闁搞劏顕ч埞鍐礋椤栨稈鎷婚梺绋挎湰椤ㄥ懏绂嶆ィ鍐┾拺闁革富鍘愮憴鍕垫闁归棿鐒﹂崐鍫曟煟濡偐甯涢柣鎾寸懇閹鈽夊▍顓т邯楠炴牠骞栨担鍦帗閻熸粍绮撳畷婊堝Ω閳轰胶顔嗛梺璺ㄥ櫐閹凤拷
    Copyright 2021 零零教育信息网 @ Powered By 零零教育信息网 ，这是一个公共的免费分享平台
    网站导航联系我们广告合作豫ICP备09039788号
    个人中心
    服务邮箱

    服务邮箱

    7720015@qq.com

    微信咨询
    我的网站名称
    返回顶部
    X我的网站名称

    截屏，微信识别二维码

    微信号：ten00_cn

    （点击微信号复制，添加好友）

      打开微信

    微信号已复制，请打开微信添加咨询详情！