一根长度为L的轻质直杆两端各固定一个可视为质点的小球A和B，两小球质量均为m，直杆可以绕过其中点O的水平轴在竖直平面内匀速转动，若直杆匀速转动周期为2πLg，求（1）小球转动

首页 > 考试 > 物理 > 高中物理 > 牛顿第三定律/2022-10-30 / 加入收藏 / 阅读 [打印]

◎ 题目

一根长度为L的轻质直杆两端各固定一个可视为质点的小球A和B，两小球质量均为m，直杆可以绕过其中点O的水平轴在竖直平面内匀速转动，若直杆匀速转动周期为2π

L
g
，求
（1）小球转动的角速度；
（2）直杆转动到如图竖直位置时，A、B两小球对直杆作用力各多大？方向如何？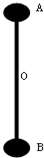
魔方格

◎ 答案

（1）已知小球的转动周期T=2π

L
g
，
故小球转动的角速度ω=
2π
T
=

g
L
…①
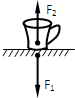
（2）以A小球为研究对象，在最高点的受力如图，设NA方向向上，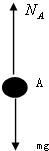

魔方格

根据牛顿第二定律得：mg-NA=mω2
L
2
…②
由①②式得：NA=
1
2
mg…③
根据牛顿第三定律得，A球对直杆有竖直向下的压力，
大小为NA′=NA=
1
2
mg…④

魔方格

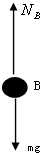以B小球为研究对象，在最低点的受力如图，设NB方向向上，根据牛顿第二定律得：NB-mg=mω2
L
2
…⑤
由①⑤式得：NB=
3
2
mg…⑥
根据牛顿第三定律得，B球对直杆有竖直向下的拉力，
大小为NB′=NB=
3
2
mg…⑦
故A球对直杆有竖直向下的压力，大小为
1
2
mg．B球对直杆有竖直向下的拉力，大小为
 1/2    1 2 下一页 尾页
质直 中点 一根 知识点 两端
  • 最新内容
  • 相关内容
  • 网友推荐
  • 图文推荐
  • 汽车拉着拖车在水平道路上沿直线加(2022-10-30)
  • 汽车拉着拖车在水平道路上沿直线加(2022-10-30)
  • 关于牛顿第三定律，以下说法中正确(2022-10-30)
  • 用计算机辅助实验系统（DIS）做验证(2022-10-30)
  • 根据牛顿第三定律可以判断，下列说(2022-10-30)
  • 用计算机辅助实验系统做验证牛顿第(2022-10-30)
  • 牛顿第三定律所阐明的作用力与反作(2022-10-30)
  • 已知某透镜的焦距为1cm的整数倍。将(2022-10-30)
  • 甲、乙两队拔河，甲胜乙败，下列叙(2022-10-30)
  • 如图所示：质量不计的杆O1B和O2A，长度均为l、O1和O2为
  • 用一根轻质弹簧竖直悬挂一小球，小球和弹簧的受力如图
  • 物体A被一根轻弹簧悬于天花板下，画出重物和弹簧的受力
  • 如图所示，质量为m的小球，用一根长为L的绳吊起来，放
  • 如图所示，一物体被一根轻绳悬挂在天花板下处于静止状
  • 电灯悬挂在一根绳子下保持静止，则绳子对电灯的拉力（
  • 某青年的质量是某少年质量的两倍，该青年能施的最大拉
  • 一根长为L的轻杆下端固定一个质量为m的小球，上端连在
  • 据《城市快报》报道，在一个动物园门前，停放着一辆1.
  • 如图所示，一玩滚轴溜冰的小孩（可视作质点）质量为m=
  • 机车A拉着车厢B向右行驶，用FAB和F(2022-10-30)
  • 若飞机在起飞时不慎撞到了一只鸟，(2022-10-30)
  • 如图甲所示为利用DIS做验证牛顿第三(2022-10-30)
  • 一物体静止在桌面上，则（）A．物体(2022-10-30)
  • 对于静止在水平桌面上的物体，以下(2022-10-30)
  • 关于作用力和反作用力以及一对平衡(2022-10-30)
  • 关于一对作用力与反作用力在作用过(2022-10-30)
  • 如图所示，杯子放在水平桌面时，杯(2022-10-30)
  • 关于作用力与反作用力，下列说法中(2022-10-30)
  • 下列说法中正确的是（）A．公式a=△(2022-10-30)
    • 如图甲所示为利用DIS做验证牛顿第三定律实验的操作示意图，该实验所用的传感器为______．图乙为实验时在软件界面上出现的结果，观察图乙我们可以得出：作用力与反作用力总是：_
    如图甲所示为利用DIS做验证牛    		如图所示，杯子放在水平桌面时，杯子对桌面的压力为F1，桌面对杯子的支持力为F2，则下列说法正确的是（）A．力F1就是杯子的重力B．力F1和力F2是一对平衡力C．力F1和力F2是一对作用
    如图所示，杯子放在水平桌面    		如图所示，质量为0.2kg的物体带正电，其电量为4×10-4C，从半径为0.3m光滑的14圆弧滑轨上端A点由静止下滑到底端B点，然后继续沿水平面滑动．物体与水平面间的滑动摩擦系数为
    如图所示，质量为0.2kg的物体    		如图所示，质量为M的木板可以沿倾角为α的固定斜面无摩擦地滑下，欲使木板静止在斜面上，木板上质量为m的人应以多大的加速度向下奔跑？
    如图所示，质量为M的木板可以    		如图所示，物体A放在水平桌面上，被水平细绳拉着处于静止状态，则（）A．绳子对A的拉力小于A受的静摩擦力B．A受的重力和桌面对A的支持力是一对作用力和反作用力C．A对桌面的压力和
    如图所示，物体A放在水平桌面
    上一篇：在绳下吊一个小球保持静止状态，下列叙述中正确的是（）A．小球对绳的拉力就是球的重力B．小球对绳的拉力大小等于小球的重力，但拉力不是重力C．由于小球吊在空中，所以小球的     下一篇：在弹性海绵垫的正上方h1高处，将重为G的小球以速率v0竖直下抛，落垫后反弹的高度为h2．设球与海绵垫第一次接触的时间为t，求在此时间内球对海绵垫的平均作用力的大小．（空气阻
    零零教育社区：论坛热帖子
    栏目导航
    Copyright 2021 零零教育信息网 @ Powered By 零零教育信息网 ，这是一个公共的免费分享平台
    网站导航联系我们广告合作豫ICP备09039788号
    个人中心
    服务邮箱

    服务邮箱

    7720015@qq.com

    微信咨询
    我的网站名称
    返回顶部
    X我的网站名称

    截屏，微信识别二维码

    微信号：ten00_cn

    （点击微信号复制，添加好友）

      打开微信

    微信号已复制，请打开微信添加咨询详情！