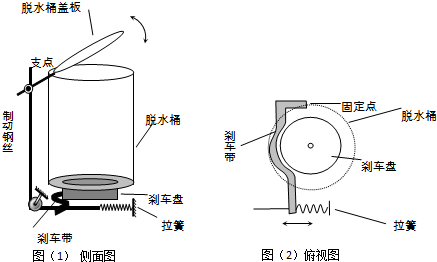
婵ê鐡ㄥΣ鎼佹儑閸忕厧鐨炬俊顖d悍缁辨繄浠︽潏銊π﹂柣顏勵槸閸㈡煡鎳曞銉㈠亾閸屾侗鍎橀梻鍌ゅ枦椤㈡垶绂嶉崫鍕闂侇叏缍€缁旂喖鏁嶉悢鐑樼畳闁活亣鍋愬▔鈺呮儎閸繍妲遍柕鍡楀€规晶鐘虫叏鐎n喒鍋撴担瑙勑氱憸鐗堝釜缁辨繈宕i崼銉㈠亾娴e憡鍋樼憸鐗堝笒楠炴捇濡撮崒婵嗩仧闁告帞澧楅惈娆撳础濡ゅ嫬鍨佸☉鎾筹攻濡差剟鏁嶇仦钘夌.濞戞挸娲ら幏浼村及閵夈倗绉堕柕鍡嫹
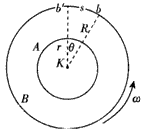
如图所示,按顺时针方向在竖直平面内作匀速转动的轮子边缘上有一点A.当A通过与圆心等高的a点时,有一质点B从圆心O开始做自由落体运动.已知圆的半径为R,求:(1)轮子的角速度ω

◎ 题目
| 如图所示,按顺时针方向在竖直平面内作匀速转动的轮子边缘上有一点A.当A通过与圆心等高的a点时,有一质点B从圆心O开始做自由落体运动.已知圆的半径为R,求: (1)轮子的角速度ω满足什么条件时,点A才能与B相遇? (2)轮子的角速度ω满足什么条件时,点A与B的速度才会相同?  |
◎ 答案
(1)质点从B点做自由落体运动,根据R=
t=
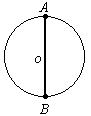
A和B只能在d点相遇,所以A运动的时间为(n+
所以(n+
解得:ω=2π(n+
(2)点A与B的速度相同的位置只能在c点, 则t=(n+1)T, 根据速度相等有:ωR=gt=g(n+1)
解得:ω=
答:(1)轮子的角速度ω=2π(n+
|

![如图所示,有一皮带传动装置,A、B、C三点到各自转轴的距离分别为RA、RB、RC,已知RB=RC=RA/2,若在传动过程中,皮带不打滑。则[]A、A点与C点的角速度大小相等B、A点与C点的](http://www.00-edu.com/d/file/2022-09-22/4f3c88b50c2fa903804d354d5b1fdc83.png)