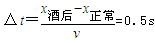濮樺瓨妲搁惇鍏煎皾濡亷绱濈仦杈ㄦЦ閻鍢查懕姘モ偓鍌涱儘闂傤喛顢戞禍鍝勫箵闁綀绔熼敍鐔烘箒閻偐娉╅惄鍫濐槱閵嗗倹澧犳慨瀣偓浣规К瑜版帪绱濋崣鍫モ偓浣告偘瑜版帒骞撻妴鍌濆閸掔増鐫欓崡妤勫垁娑撳﹥妲敍灞藉磮娑撳洤鎷伴弰銉ょ秶閵嗭拷
如图所示,长l=1.6m的细线一端固定在O点,另一端栓着一质量m=0.1kg的摆球.让摆球由A位置静止下摆,已知OA与竖直方向OBC的夹角为600求:(1)摆球摆到最低点B位置时线的拉力,

◎ 题目
| 如图所示,长l=1.6m的细线一端固定在O点,另一端栓着一质量m=0.1kg的摆球.让摆球由A位置静止下摆,已知OA与竖直方向OBC的夹角为600求: (1)摆球摆到最低点B位置时线的拉力, (2)若悬点O到地面的竖直高度为H=6.6m,球摆到B点时细线刚好被拉断,则摆球落地时的速度大小以及落地点D到C点的距离(g=10m/s2)  |
◎ 答案
(1)摆球由A位置摆到最低点B位置的过程中,由机械能守恒定律得 mgl(1-cos60°)=
得到摆球到最低点B位置时的速度v=
摆球经过B位置时,根据牛顿第二定律得,T-mg=m
得到 T=mg+m
(2)球摆到B点时细线被拉断后,摆球做平抛运动,平抛运动的高度为h=H-l=5m,由机械能守恒定律得 mgh+
得到摆球落地时的速度大小V=
代入解得 V=2
将平抛运动分解为水平方向和竖直方向两个分运动,竖直方向做自由落体运动,则有 h=
水平方向做匀速直线运动,则DC间距离x=vt=v
|