如图1,在正方形ABCD中,点E、F分别为边BC、CD的中点,AF、DE相交于点G,则可得结论:①AF=DE,②AF⊥DE(不须证明).(1)如图②,若点E、F不是正方形ABCD的边BC、CD的中点,但满足C-数学-00教育-零零教育信息网
题文
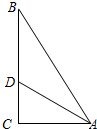
如图1,在正方形ABCD中,点E、F分别为边BC、CD的中点,AF、DE相交于点G,则可得结论:①AF=DE,②AF⊥DE(不须证明).
(1)如图②,若点E、F不是正方形ABCD的边BC、CD的中点,但满足CE=DF,则上面的结论①、②是否仍然成立;(请直接回答“成立”或“不成立”)
(2)如图③,若点E、F分别在正方形ABCD的边CB的延长线和DC的延长线上,且CE=DF,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.
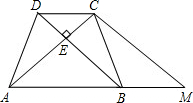
(3)如图④,在(2)的基础上,连接AE和EF,若点M、N、P、Q分别为AE、EF、FD、AD的中点,请先判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种,并写出证明过程.

|
题型:解答题 难度:中档
答案
(1)∵DF=CE,AD=DC,且∠ADF=∠DCE,
∴△DEC≌△AFD;
∴结论①、②成立(1分)
(2)结论①、②仍然成立.理由为:
∵四边形ABCD为正方形,
∴AD=DC=CB且∠ADC=∠DCB=90°,
在Rt△ADF和Rt△ECD中
,
∴Rt△ADF≌Rt△ECD(SAS),(3分)
∴AF=DE,
∴∠DAF=∠CDE,
∵∠ADE+∠CDE=90°,
∴∠ADE+∠DAF=90°,
∴∠AGD=90°,
∴AF⊥DE;(5分)
(3)结论:四边形MNPQ是正方形(6分)
证明:∵AM=ME,AQ=QD,
∴MQ∥DE且MQ=DE,
同理可证:PN∥DE,PN=DE;MN∥AF,MN=AF;PQ∥AF,PQ=AF;
∵AF=DE,
∴MN=NP=PQ=QM,
∴四边形MNPQ是菱形,(8分)
又∵AF⊥DE,
∴∠MQP=90°,
∴四边形MNPQ是正方形.(10分) |
据专家权威分析,试题“如图1,在正方形ABCD中,点E、F分别为边BC、CD的中点,AF、DE相交..”主要考查你对 直角三角形的性质及判定,正方形,正方形的性质,正方形的判定 等考点的理解。关于这些考点的“档案”如下:
直角三角形的性质及判定正方形,正方形的性质,正方形的判定
考点名称:直角三角形的性质及判定
考点名称:正方形,正方形的性质,正方形的判定


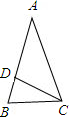
 。如图,∠BAC=90°,则AB2+AC2=BC2(勾股定理)
。如图,∠BAC=90°,则AB2+AC2=BC2(勾股定理)
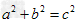 ,那么这个三角形就是直角三角形。(勾股定理的逆定理)。
,那么这个三角形就是直角三角形。(勾股定理的逆定理)。