水是眼波横,山是眉峰聚。欲问行人去那边?眉眼盈盈处。才始送春归,又送君归去。若到江南赶上春,千万和春住。
(1)计算:11×3+13×5+…+12011×2013;(2)若|x-1|+|y+1|=0,试求:1x(y+3)+1(x+1)(y+4)+1(x+2)(y+5)+…+1(x+2011)(y+2014)的值;(3)若n为整数,且(11×4+14×7+17×10+…+12002×2005)×-数学
1(x+2)(y+5)+…+
| 1 |
| (x+2011)(y+2014) |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2012 |
| 1 |
| 2013 |
=1-
| 1 |
| 2013 |
=
| 2012 |
| 2013 |
(3)
| 1 |
| 1×4 |
| 1 |
| 4×7 |
| 1 |
| 7×10 |
| 1 |
| 2002×2005 |
=
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 7 |
| 1 |
| 2002 |
| 1 |
| 2005 |
=
| 1 |
| 3 |
| 1 |
| 2005 |
=
| 1 |
| 3 |
| 2004 |
| 2005 |
=
| 668 |
| 2005 |
∵(
| 1 |
| 1×4 |
| 1 |
| 4×7 |
| 1 |
| 7×10 |
| 1 |
| 2002×2005 |
∴n=-3或-2或-1或0或1或2或3,
∴当n=-3时,n2+n=6;
当n=-2时,n2+n=2;
当n=-1时,n2+n=0;
当n=0时,n2+n=0;
当n=1时,n2+n=2;
当n=2时,n2+n=6;
当n=3时,n2+n=12.
据专家权威分析,试题“(1)计算:11×3+13×5+…+12011×2013;(2)若|x-1|+|y+1|=0,试求:1x(..”主要考查你对 绝对值,代数式的求值 等考点的理解。关于这些考点的“档案”如下:
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

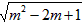
![|﹣2|的相反数是[]A.B.﹣2C.D.2-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/5/2019-02-14/483ef5564b74ffa1cd874b00dbe1b33c.png)
![﹣3的绝对值是[]A.﹣3B.3C.±3D.﹣-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/5/2019-02-14/b1a26a66a91bad435fae1499676c002f.png)


