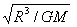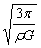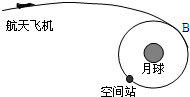
作为我国对月球实施无人探测的第二阶段任务，“嫦娥二号”卫星预计在2011年前发射，登月器也将指日登陆月球．质量为m的登月器与航天飞机连接在一起，随航天飞机绕月球做半径为3
◎ 题目
| 作为我国对月球实施无人探测的第二阶段任务，“嫦娥二号”卫星预计在2011年前发射，登月器也将指日登陆月球．质量为m的登月器与航天飞机连接在一起，随航天飞机绕月球做半径为3R（ R为月球半径）的圆周运动．当它们运行到轨道的A点时，登月器被弹离，航天飞机速度变大，登月器速度变小且仍沿原方向运动，随后登月器沿椭圆登上月球表面的B点，在月球表面逗留一段时间后，经快速起动仍沿原椭圆轨道回到分离点A并立即与航天飞机实现对接．已知月球表面的重力加速度为g月．试求： （1）登月器与航天飞机一起在圆周轨道上绕月球运行的周期是多少？ （2）若登月器被弹射后，航天飞机的椭圆轨道半长轴为4R，则为保证登月器能顺利返回A点，登月器可以在月球表面逗留的时间是多少？  |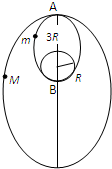
◎ 答案
| （1）设登月器和航天飞机在半径3R的轨道上运行时的周期为T， 因其绕月球作圆周运动， 所以应用牛顿第二定律有 G
在月球表面的物体所受重力近似等于万有引力， 即G
联立①②解得T=6π
（2）设登月器在小椭圆轨道运行的周期是T1，航天飞机在大椭圆轨道运行的周期是T2． 对登月器和航天飞机依据开普勒第三定律分别有
为使登月器仍沿原椭圆轨道回到分离点与航天飞机实现对接，登月器可以在月球表面逗留的时间t应满足 t=nT2-T1 （其中，n=1、2、3、…）…⑥ 联立③④⑤⑥得 t=4π(4n-
|
