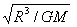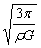我们的银河系的恒星中大约四分之一是双星.某双星由质量不等的星体S1和S2构成,两星在相互之间的万有引力作用下绕两者连线上某一定点C做匀速圆周运动.由天文观察测得其运动周
◎ 题目
我们的银河系的恒星中大约四分之一是双星.某双星由质量不等的星体S1和S2构成,两星在相互之间的万有引力作用下绕两者连线上某一定点C做匀速圆周运动.由天文观察测得其运动周期为T,S1到C点的距离为r1,S1和S2的距离为r,已知引力常量为G.由此可求出S2的质量为( )
|
◎ 答案
| 设星体S1和S2的质量分别为m1、m2, 星体S1做圆周运动的向心力由万有引力提供得:
即 m2=
故选D. |
◎ 解析
“略”◎ 知识点
专家分析,试题“我们的银河系的恒星中大约四分之一是双星.某双星由质量不等的星体S1和S2构成,两星在相互之间的万有引力作用下绕两者连线上某一定点C做匀速圆周运动.由天文观察测得其运动周…”主要考查了你对 【万有引力定律的其他应用】 等知识点的理解和应用能力。关于这些知识点的“档案”,你可以点击相应的链接进行查看和学习。- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:2005年10月12日,我国成功地发射了“神舟”六号载人宇宙飞船,飞船进入轨道运行若干圈后成功实施变轨进入圆轨道运行.经过了近5天的运行后,飞船的返回舱顺利降落在预定地点.设
下一篇:如图所示,在同一轨道平面上有三颗人造地球卫星A、B、C(轨道均是圆),某一时刻它们恰好在同一直线上,则下列说法正确的是()A.根据v=gr可知vA<vB<vCB.根据万有引力定律,可知
零零教育社区:论坛热帖子
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |